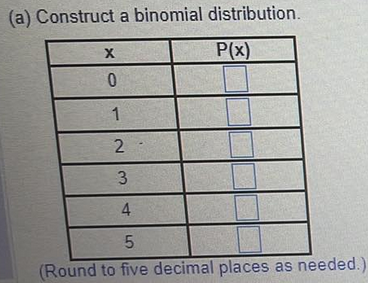
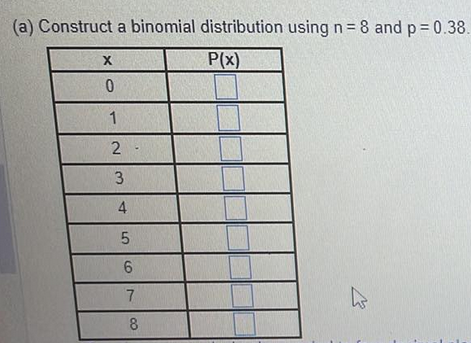
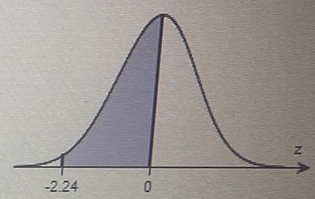
Find the indicated probability using the standard normal distribution
Qn18 Find the indicated probability using the standard normal distribution
P(-1.16 < z < 1.16)
Qn19. Assume the random variable x is normally distributed with mean mu = 50 and standard deviation sigma = 7. Find the indicated probability.
P(x > 43)
Qn20. Use the normal distribution of SAT critical reading scores for which the mean is 514 and the standard deviation is 121. Assume the variable x is normally distribted.
a. What percentage of the SAT verbal scores are less than 550?
b. If 1000 SAT verbal scores are randomly selected, about how many would you expect to be greater than 525?