ANOVA Minitab Consider a manufacturing plant that produces high-quality products
Data Analysis Using Minitab
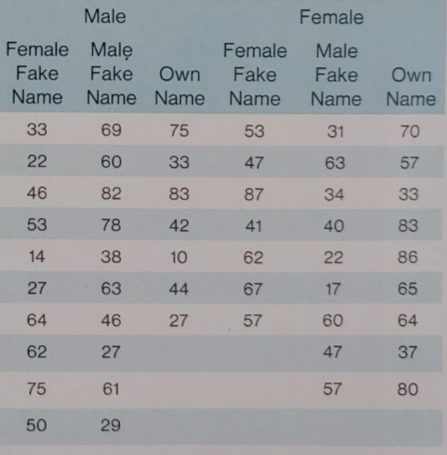
(Using Minitab Answer the following) Consider a manufacturing plant that produces high-quality products primarily using skilled labor. They are concerned about defects found in the surface coating for their product and have been exploring potential improvement strategies. Note that each prompt below may require more than one visualization and/or analysis to fully answer.
- Previous study showed that there is a difference in Quality ratings based on the Team. Considering this, they would like to test four potential factors (Line, Method, Temperature, and Humidity) while controlling for the effect of Team. Using the provided data, create a 2k factorial model by restructuring the Method factor as two, two-level factors and treating Team as a four-level blocked variable. Use Minitab to generate a 25-2 model blocked by replicates and extract the relevant data from the provided dataset to complete the analysis. Discuss the validity, fit, and reliability of the model and interpret the results including addressing any important aliased relationships.
- Identify the treatment combinations that would be needed to complete the full fold-over for this design and briefly discuss how the fold-over model would help to interpret the results from Part 2. Complete the full fold-over, discuss the validity, fit, and reliability of the model, and interpret the results.
- Use a general full factorial DOE model to evaluate the original five factors using their defined levels (a mixed-level design). Discuss the validity, fit and reliability of the model and interpret the results.