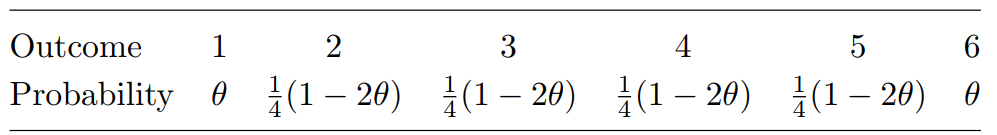In this section we will turn our attention to comparing two population proportions. Once again, there are times when we aren't necessarily focused on the exact proportion, but rather how proportions from two populations compare, that is, if they are equal, or if one is larger than the other.

When we were comparing population means, we constructed a confidence interval for the difference between the two population means. Similarly, when comparing two population proportions, we use a confidence interval for the difference between the population proportions. The best point estimate for the difference is pˆ1−pˆ2

. In this section we will restrict our discussion to comparing two population proportions when the following conditions are met. Notice that the conditions are similar to those discussed for estimating a single population proportion.

All possible samples of a given size have an equal probability of being chosen; that is, simple random samples are used.

The samples are independent.

The conditions for a binomial distribution are met for both samples.

The sample sizes are large enough to ensure that n1pˆ1≥5

, n1(1−pˆ1)≥5, n2pˆ2≥5, and n2(1−pˆ2)≥5

.

When these conditions are met, we can apply the Central Limit Theorem to the sampling distribution of the differences between the sample proportions for two independent samples. This means that we will use the standard normal distribution to calculate the margin of error of a confidence interval for the difference between two population proportions. You can assume that the necessary criteria are met for all examples and exercises in this lesson.
Memory Booster

Population Proportion

p=xN=# of successespopulation size

Sample Proportion

pˆ=xn=# of successessample size

Properties of a Binomial Distribution

    The experiment consists of a fixed number, n, of identical trials.

    Each trial is independent of the others.

    For each trial, there are only two possible outcomes. For counting purposes, one outcome is labeled a success, and the other a failure.

    For every trial, the probability of getting a success is called p. The probability of getting a failure is then 1−p

.

The binomial random variable, X, counts the number of successes in n trials.

If there are n pairs of data values and the population distribution of the paired differences is approximately normal, then the sampling distribution for the sample statistic d⎯⎯ follows a t-distribution with n, n−1 degrees of freedom. Hence, the formula for the margin of error is as follows. This is the same formula that is used when estimating a single population mean when σ is unknown. This is because we use the paired differences as a single set of sample data rather than using the data from the two samples separately when working with paired data.
Margin of Error of a Confidence Interval for the Mean of the Paired Differences for Two Populations ( σ Unknown, Dependent Samples)

When both population standard deviations are unknown, the samples taken are dependent, simple random samples of paired data, and either the number of pairs of data values in the sample data is greater than or equal to 30

or the population distribution of the paired differences is approximately normal, the margin of error of a confidence interval for the mean of the paired differences for two populations is given by

E=(tα2/)(sdn⎯⎯√)

where tα2/
is the critical value for the level of confidence, c=1−α such that the area under the t-distribution with n−1 degrees of freedom to the right of tα2/ is equal to α2

.

sd

is the sample standard deviation of the paired differences for the sample data, an

n is the number of paired differences in the sample data.

To use paired data to construct a confidence interval, the following conditions must be met.

All possible samples of a given size have an equal probability of being chosen; that is, simple random samples are used.

The samples are dependent.

Both population standard deviations, σ1

and σ2

are unknown.

Either the number of pairs of data values in the sample data is greater than or equal to 30
(n≥30)

or the population distribution of the paired differences is approximately normal.

In this lesson, you may assume that these conditions are met for all examples and exercises involving paired data.

The value that we want to estimate is the mean of the paired differences for the two populations of dependent data, μd
. Recall that the first step in constructing a confidence interval is to find the point estimate, and the best point estimate for a population mean is a sample mean. Therefore, the mean of the paired differences for the sample data, d⎯⎯

is the point estimate used here.

Formula: Mean of Paired Differences

When two dependent samples consist of paired data, the mean of the paired differences for the sample data is given by

d⎯⎯=∑din

where di

is the paired difference for the ith pair of data values and

n is the number of paired differences in the sample data.

Faculty of Science, Technology, Engineering and Mathematics M248 Analysing data

Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.

You are advised to look at the general advice on answering TMAs provided on the M248 website. Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions.

Note that the Minitab files that you require for TMA 05 are not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website.

Question 1, which covers topics in Unit 9, and Question 2, which covers topics in Unit 10, form M248 TMA 05. Question 1 is marked out of 32; Question 2 is marked out of 18.

Minitab Question one
You should be able to answer this question after working through Unit 9.
(a) A study was undertaken to examine the tensile strength of a new type of polyester fibre. The Minitab worksheet polyester-fibre.mtw gives the breaking strengths (in grams/denier, denier being a unit of fineness) of a random sample of n = 30 observations, given in the variable Strength.

The existing type of polyester fibre which the new type is designed to replace has a mean breaking strength of 0.26 grams/denier. Interest centres on using the data in polyester-fibre.mtw to test whether the mean breaking strength of the new type of polyester fibre differs from the mean breaking strength of the existing type of polyester fibre.

(i) Write down appropriate null and alternative hypotheses for a test of whether the mean breaking strength of the new type of polyester fibre differs from the mean breaking strength of the existing type of polyester fibre. Define any notation that you use. [3]

(ii) It is proposed to use a z-test to test the hypotheses specified in part (a)(i). Justify this choice of test in terms of the sample size, n. [1]

(iii) Write down the formula for the test statistic used in the z-test of part (a)(ii). Define any further notation that you use. [2]

(iv) Write down the null distribution of the test statistic in part (a)(iii). What is the reason for the use of the word ‘null’ in the phrase ‘null distribution’? [2]

(v) Using Minitab, obtain the standard deviation of the values in Strength, then perform the z-test that you have been considering throughout part (a) of this question. Provide a copy of the **Minitab
output** produced by performing this test. (This output should comprise four lines which start with the words Test, The, Variable and Strength, respectively.) [3]

(vi) Interpret the result of the test that you have just performed, as given by its p-value. [3]
(vii) Would you have rejected H0 or not rejected H0 if you had tested the hypotheses of interest in this question at the 5% significance level? Would you have rejected H0 or not rejected H0 if you had tested these hypotheses at the 1% significance level? Justify each of your answers separately. [4]

(b) The proportion, p0, of foraging bumblebees not exposed to pesticides who bring very little pollen back to their nest is 0.4. A recent study of foraging bumblebees investigated the effect of exposure to a widely used neonicotoid pesticide called imidacloprid on pollen foraging rates. (Neonicotoid pesticides are commonly used in agriculture due to their low toxicity in mammals.) Let p denote the proportion of foraging bumblebees exposed to imidacloprid who bring very little pollen back to their nest.

A sample of 60 bumblebees were exposed to a low (field realistic) dose of imidacloprid: 39 of these bumblebees brought back very little pollen to their nest. Use these data to perform the test of the hypotheses H0 : p = 0:4; H1 : p > 0:4; by working through the following subparts of this part of the question.

(i) Calculate the observed value of the test statistic for this test. [2]
(ii) Using the approximate normal null distribution of this test statistic, identify the rejection region of a test of the stated hypotheses using a 1% significance level. [2]
(iii) Report and interpret the outcome of this hypothesis test. [2]

(c) The isotopic abundance ratio of natural silver (Ag) is the ratio of the stable isotopes Ag107 to Ag109. Its mean is 1.076 and measurements on a random sample of observed isotopic abundance ratios suggested that they are plausibly normally distributed with a sample standard deviation of 0.0026. Interest in this part of the question concerns the planning of a further experiment to detect whether this ratio is different in observations from a certain source of silver nitrate. The new study will use a two-sided test at the 5% significance level, assuming normality. It is desired to make sufficient observations of the isotopic abundance ratio on the silver nitrate so that the power of the test to distinguish a difference between the null hypothesis of a true underlying mean of 1.076 and a value that is 0.0015 larger or 0.0015 smaller is 90%. For the purpose of performing the necessary sample size calculation, it will be assumed that the population standard deviation of the isotopic abundance ratio measurements is equal to the sample standard deviation given above.

(i) Calculate, by hand, the size of the sample required to achieve the desired power of the test. Show our working. [6]

(ii) Ignoring rounding up to an integer, and assuming that no other aspect of the problem changes, by what multiple is the required sample size changed if, instead of seeking to distinguish between the underlying mean and values that are 0.0015 larger or smaller than it, it was decided to seek to distinguish between the underlying mean and values that are 2/3 as much (that is, 0.001) larger or smaller than it? [2]

Minitab statistics question 2
Question 2 { 18 marks
You should be able to answer this question after working through Unit 10.
(a) Halofenate has been shown to be effective in the treatment of conditions associated with abnormally high levels of lipids in the blood; triglyceride is a lipid of particular importance. A group of 22 patients were treated with halofenate medication. The changes between the patients’ triglyceride levels after treatment with halofenate and before treatment with halofenate were measured. These changes are in the Minitab worksheet triglyceride.mtw, in the column Halofenate. (Note that a negative change corresponds to the desirable outcome of a reduction in triglyceride levels.)

The column Placebo contains the changes between triglyceride levels after treatment with an inactive placebo and before treatment with the placebo, for an independently drawn control group of 21 patients. The main question of interest is whether halofenate makes a more favourable change to triglyceride levels, in comparison to a placebo.

Graphical investigation of the data shows that normality cannot be assumed for the distribution of either Halofenate or Placebo. It is therefore decided to compare the effects of halofenate and a placebo on
triglyceride reduction using the Mann{Whitney test.

(i) Write down appropriate null and alternative hypotheses for a test of whether the difference between the location of the changes between triglyceride levels after and before treatment with halofenate and the location of the changes between triglyceride levels after and before treatment with a placebo is negative. Define any notation that you use. [3]

(ii) Use Minitab to carry out the Mann-Whitney test of the hypotheses discussed above. Provide a copy of one line of the Minitab output which includes the p-value associated with the test. [2]

(iii) Interpret the result of the test that you have just performed, as given by its p-value. [2]
(b) In Table 5 of Unit 3, data were given on the month of death (January = 1, February = 2, . . . , December = 12) for 82 descendants of Queen Victoria; they all died of natural causes. The data are repeated here in Table 1.

The question of whether or not these royal deaths could be claimed to be from a discrete uniform distribution on the range 1; 2; : : : ; 12 was considered informally in Example 20 of Unit 3 and, at some length, in Chapter 8 of Computer Book A. From these investigations, it looked as though the discrete uniform distribution may be a plausible model for these data, but no firm conclusion was reached.

In this part of the question, you are going to perform a chi-squared goodness-of-fit test of the discrete uniform distribution to these data.

(i) Obtain the expected frequencies of the values 1; 2; : : : ; 12 assuming a discrete uniform distribution. Why is it not necessary to pool categories before performing a chi-squared goodness-of-fit test in this case? [3]

(ii) Carry out the remainder of the chi-squared goodness-of-fit test: report the individual elements of the chi-squared test statistic, the value of the test statistic itself, the number of degrees of freedom of the chi-squared null distribution, and whatever this tells you about the p-value associated with the test. Interpret the outcome of the test.

m248 TM 05 sample statistics solution.docx

Let us know if you like us to help you with any of your coursework,

Faculty of Science, Technology, Engineering and MathematicsM248 Analysing data

M248 - TMA 04

*Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.
You are advised to look at the general advice on answering TMAs provided on the M248 website. Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions. Note that one of the Minitab files that you require for TMA 04 is not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website. For your convenience, the other Minitab file required for TMA 04, which already appeared in the module, is also available for download from the ‘Assessment’ area.*

Question 1, which covers topics in Unit 7, and Question 2, which covers topics in Unit 8, form M248 TMA 04. Question 1 is marked out of 23; Question 2 is marked out of 27.

Question 1 { 23 marks
You should be able to answer this question after working through Unit 7.
(a) Let X and Y be independent random variables both with the same
mean µ 6= 0. Define a new random variable W = aX + bY where a and
b are constants.
(i) Obtain an expression for E(W). [2]
(ii) What constraint is there on the values of a and b so that W is an
unbiased estimator of µ? Hence write all unbiased versions of W as
a formula involving a, X and Y only (and not b). [3]
(b) An otherwise fair six-sided die has been tampered with in an attempt to
cheat at a dice game. The effect is that the 1 and 6 faces have different
probability of occurring than the 2, 3, 4 and 5 faces.
Let θ be the probability of obtaining a 1 on this biased die. Then, the
outcomes of rolling the biased die have the following probability mass
function.
Table 1 The p.m.f. of outcomes of rolls of a biased die:

(i) By consideration of the p.m.f. in Table 1, explain why it is necessary for θ to be such that 0 < θ < 1=2. [2]
(ii) The value of θ is unknown. Data from which to estimate the value of θ were obtained by rolling the biased die 1000 times. The result of this experiment is shown in Table 2.

Table 2 Outcomes of 1000 independent rolls of a biased die

Show that the likelihood of θ based on these data is
L(θ) = C θ395 (1 − 2θ)605 where C is a positive constant, not dependent on θ. [5]
(iii) Show that L0(θ) = C θ394(1 − 2θ)604 (395 − 2000 θ): [4]

(iv) What is the value of the maximum likelihood estimate, θb, of θ based on these data? Justify your answer. What does the value of θb suggest about the value of θ for this biased die compared with the
value of θ associated with a fair, unbiased, die? [4]

c) Studies of the size and range of wild animal populations often involve tagging observed individual animals and recording how many times each is caught in a trap (from which it is then released back into the wild). The dataset presented in Table 3 consists of the numbers of times each of n = 334 wood mice were caught in a particular trap (over a two-year time period). The data are also provided in the Minitab file wood-mice.mtw.

Table 3 Numbers of trappings of wood mice

The geometric distribution with parameter p is a good model for these data.
(i) What is the maximum likelihood estimator of p for a geometric model? [1]
(ii) What is the maximum likelihood estimate of p for the data in Table 3? You are recommended to use Minitab to help you to answer this part of the question. [2]

Question 2 in Statistics
You should be able to answer this question after working through Unit 8.
(a) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)

Modern aircraft cockpit windscreens are complex items, comprising several layers of material and a heating system. Such windscreens are replaced upon damage to any of their components. A dataset was collected on the times to replacement of n = 84 windscreens of a particular modern airliner. The sample mean windscreen replacement time was 23 515 hours of flight. The sample standard deviation of windscreen replacement times was 5168 hours of flight.

(i) Obtain an approximate 90% confidence interval for the mean replacement time of this type of aircraft windscreen. What
property of the dataset justifies using this type of confidence interval, and why? [6]
(ii) Interpret the particular confidence interval that you found in part (a)(i) in terms of repeated experiments. [3]

(b) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)
In a large study of patients who were being treated for hypertension (high blood pressure), 148 out of 5493 patients receiving the conventional treatment for hypertension later suffered a stroke. Also,
192 out of 5492 patients receiving an alternative drug to treat their hypertension later suffered a stroke

(i) Obtain an approximate 95% confidence interval for the difference in proportions between the number of conventionally treated hypertension patients who later suffered a stroke and the number of hypertension patients treated with the alternative drug who later suffered a stroke. (You are advised to work with proportions rounded to four decimal places throughout; also, you may assume that the numbers involved are large enough that your approximation is a good one.) [5]

(ii) Some clinicians had suggested that the proportions of hypertension patients who suffered a stroke would not depend on which treatment they were being given. Are the data consistent with that
suggestion? Justify your answer briefly. [2]

(c) In various places in this module, data on the silver content of coins minted in the reign of the twelfth-century Byzantine king Manuel I Comnenus have been considered. The full dataset is in the Minitab file coins.mtw. The dataset includes, amongst others, the values of the silver content of nine coins from the first coinage (variable Coin1) and seven from the fourth coinage (variable Coin4) which was produced a number of years later. (For the purposes of this question, you can ignore the variables Coin2 and Coin3.) In particular, in Activity 8 and Exercise 2 of Computer Book B, it was argued that the silver contents in both the first and the fourth coinages can be assumed to be normally distributed. The question of interest is whether there were differences in the silver content of coins minted early and late in Manuel’s reign. You are about to investigate this question using a two-sample t-interval.

(i) Using Minitab, find either the sample standard deviations of the two variables Coin1 and Coin4, or their sample variances. Hence, check for equality of variances using the rule of thumb given in
Subsection 4.4 of Unit 8. [3]

(ii) Whatever the outcome of part (c)(i), use Minitab to obtain a 90% two-sample t-interval for the difference E(X1) − E(X4) where X1 denotes the mean silver content in coins of the first coinage and X4
denotes the mean silver content in coins of the fourth coinage.

State that interval and comment briefly on what it tells us about the silver content of coins in the earlier and later coinages. [3]

(iii) Name the distribution used in constructing the confidence interval in part (c)(ii), state the value of its parameter and show why the parameter takes the value that it does. [2]
(iv) What would have been the outcome if you had obtained a 90% two-sample t-interval for E(X4) − E(X1) instead of for

E(X1) − E(X4)? Justify your conclusion in terms of the derivative of the parameter transformation involved. [3]

If you need someone to help you with this statistics assignment, then MyMathLab homework help is the right platform to address all your statistics needs.