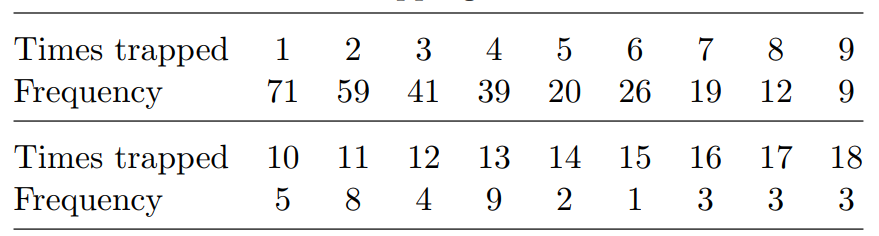
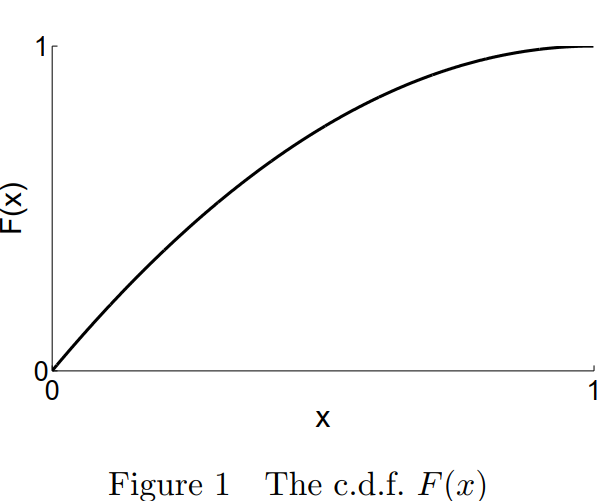
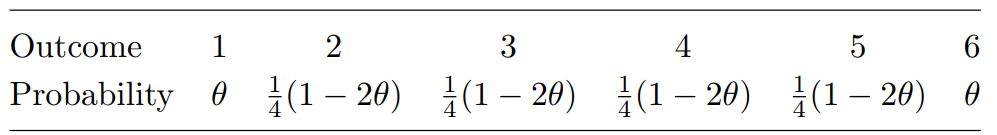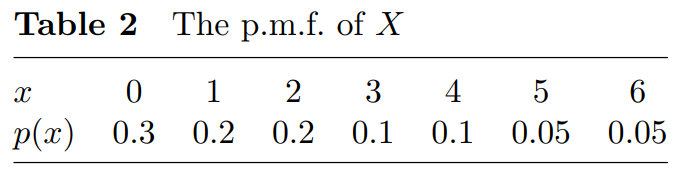Open Statistics Assignment - M248 TMA 05
Faculty of Science, Technology, Engineering and Mathematics M248 Analysing data
Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.
You are advised to look at the general advice on answering TMAs provided on the M248 website. Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions.
Note that the Minitab files that you require for TMA 05 are not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website.
Question 1, which covers topics in Unit 9, and Question 2, which covers topics in Unit 10, form M248 TMA 05. Question 1 is marked out of 32; Question 2 is marked out of 18.
Minitab Question one
You should be able to answer this question after working through Unit 9.
(a) A study was undertaken to examine the tensile strength of a new type of polyester fibre. The Minitab worksheet polyester-fibre.mtw gives the breaking strengths (in grams/denier, denier being a unit of fineness) of a random sample of n = 30 observations, given in the variable Strength.
The existing type of polyester fibre which the new type is designed to replace has a mean breaking strength of 0.26 grams/denier. Interest centres on using the data in polyester-fibre.mtw to test whether the mean breaking strength of the new type of polyester fibre differs from the mean breaking strength of the existing type of polyester fibre.
(i) Write down appropriate null and alternative hypotheses for a test of whether the mean breaking strength of the new type of polyester fibre differs from the mean breaking strength of the existing type of polyester fibre. Define any notation that you use. [3]
(ii) It is proposed to use a z-test to test the hypotheses specified in part (a)(i). Justify this choice of test in terms of the sample size, n. [1]
(iii) Write down the formula for the test statistic used in the z-test of part (a)(ii). Define any further notation that you use. [2]
(iv) Write down the null distribution of the test statistic in part (a)(iii). What is the reason for the use of the word ‘null’ in the phrase ‘null distribution’? [2]
(v) Using Minitab, obtain the standard deviation of the values in Strength, then perform the z-test that you have been considering throughout part (a) of this question. Provide a copy of the **Minitab
output** produced by performing this test. (This output should comprise four lines which start with the words Test, The, Variable and Strength, respectively.) [3]
(vi) Interpret the result of the test that you have just performed, as given by its p-value. [3]
(vii) Would you have rejected H0 or not rejected H0 if you had tested the hypotheses of interest in this question at the 5% significance level? Would you have rejected H0 or not rejected H0 if you had tested these hypotheses at the 1% significance level? Justify each of your answers separately. [4]
(b) The proportion, p0, of foraging bumblebees not exposed to pesticides who bring very little pollen back to their nest is 0.4. A recent study of foraging bumblebees investigated the effect of exposure to a widely used neonicotoid pesticide called imidacloprid on pollen foraging rates. (Neonicotoid pesticides are commonly used in agriculture due to their low toxicity in mammals.) Let p denote the proportion of foraging bumblebees exposed to imidacloprid who bring very little pollen back to their nest.
A sample of 60 bumblebees were exposed to a low (field realistic) dose of imidacloprid: 39 of these bumblebees brought back very little pollen to their nest. Use these data to perform the test of the hypotheses H0 : p = 0:4; H1 : p > 0:4; by working through the following subparts of this part of the question.
(i) Calculate the observed value of the test statistic for this test. [2]
(ii) Using the approximate normal null distribution of this test statistic, identify the rejection region of a test of the stated hypotheses using a 1% significance level. [2]
(iii) Report and interpret the outcome of this hypothesis test. [2]
(c) The isotopic abundance ratio of natural silver (Ag) is the ratio of the stable isotopes Ag107 to Ag109. Its mean is 1.076 and measurements on a random sample of observed isotopic abundance ratios suggested that they are plausibly normally distributed with a sample standard deviation of 0.0026. Interest in this part of the question concerns the planning of a further experiment to detect whether this ratio is different in observations from a certain source of silver nitrate. The new study will use a two-sided test at the 5% significance level, assuming normality. It is desired to make sufficient observations of the isotopic abundance ratio on the silver nitrate so that the power of the test to distinguish a difference between the null hypothesis of a true underlying mean of 1.076 and a value that is 0.0015 larger or 0.0015 smaller is 90%. For the purpose of performing the necessary sample size calculation, it will be assumed that the population standard deviation of the isotopic abundance ratio measurements is equal to the sample standard deviation given above.
(i) Calculate, by hand, the size of the sample required to achieve the desired power of the test. Show our working. [6]
(ii) Ignoring rounding up to an integer, and assuming that no other aspect of the problem changes, by what multiple is the required sample size changed if, instead of seeking to distinguish between the underlying mean and values that are 0.0015 larger or smaller than it, it was decided to seek to distinguish between the underlying mean and values that are 2/3 as much (that is, 0.001) larger or smaller than it? [2]
Minitab statistics question 2
Question 2 { 18 marks
You should be able to answer this question after working through Unit 10.
(a) Halofenate has been shown to be effective in the treatment of conditions associated with abnormally high levels of lipids in the blood; triglyceride is a lipid of particular importance. A group of 22 patients were treated with halofenate medication. The changes between the patients’ triglyceride levels after treatment with halofenate and before treatment with halofenate were measured. These changes are in the Minitab worksheet triglyceride.mtw, in the column Halofenate. (Note that a negative change corresponds to the desirable outcome of a reduction in triglyceride levels.)
The column Placebo contains the changes between triglyceride levels after treatment with an inactive placebo and before treatment with the placebo, for an independently drawn control group of 21 patients. The main question of interest is whether halofenate makes a more favourable change to triglyceride levels, in comparison to a placebo.
Graphical investigation of the data shows that normality cannot be assumed for the distribution of either Halofenate or Placebo. It is therefore decided to compare the effects of halofenate and a placebo on
triglyceride reduction using the Mann{Whitney test.
(i) Write down appropriate null and alternative hypotheses for a test of whether the difference between the location of the changes between triglyceride levels after and before treatment with halofenate and the location of the changes between triglyceride levels after and before treatment with a placebo is negative. Define any notation that you use. [3]
(ii) Use Minitab to carry out the Mann-Whitney test of the hypotheses discussed above. Provide a copy of one line of the Minitab output which includes the p-value associated with the test. [2]
(iii) Interpret the result of the test that you have just performed, as given by its p-value. [2]
(b) In Table 5 of Unit 3, data were given on the month of death (January = 1, February = 2, . . . , December = 12) for 82 descendants of Queen Victoria; they all died of natural causes. The data are repeated here in Table 1.
The question of whether or not these royal deaths could be claimed to be from a discrete uniform distribution on the range 1; 2; : : : ; 12 was considered informally in Example 20 of Unit 3 and, at some length, in Chapter 8 of Computer Book A. From these investigations, it looked as though the discrete uniform distribution may be a plausible model for these data, but no firm conclusion was reached.
In this part of the question, you are going to perform a chi-squared goodness-of-fit test of the discrete uniform distribution to these data.
(i) Obtain the expected frequencies of the values 1; 2; : : : ; 12 assuming a discrete uniform distribution. Why is it not necessary to pool categories before performing a chi-squared goodness-of-fit test in this case? [3]
(ii) Carry out the remainder of the chi-squared goodness-of-fit test: report the individual elements of the chi-squared test statistic, the value of the test statistic itself, the number of degrees of freedom of the chi-squared null distribution, and whatever this tells you about the p-value associated with the test. Interpret the outcome of the test.
m248 TM 05 sample statistics solution.docx
Let us know if you like us to help you with any of your coursework,