Data Analytics using Regression Model
Data Analytics using Regression Model
Suppose that a resource allocation decision is being faced whereby one must decide how many computer servers a service facility should purchase to optimize the firm’s costs of running the facility. The more servers they have, the less workers are needed. Too many servers will result in over-capacity and waste resources. The firm’s predictive analytics effort has shown a growth trend. A new facility is called for if costs can be minimized. The firm has a history of setting up large and small service facilities and has collected the 40 data points. Let’s consider the following linear model, and estimate that using the data.
Linear Model 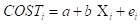
Where COST = the total cost to maintain a service facility.
X = the number of servers installed in each service facility
Using the Excel data, copy and paste to MINITAB answer the following questions.
1) Estimate the model and copy and paste the results and explain the meanings of the estimated coefficients.
2) Find TSS, RSS, ESS and R square, and carefully explain their meanings.
3) Using t test, prove/disprove if the estimated coefficient b is significant
4) What are the elasticity of server on total cost if you have 20 servers, or 40 servers?
5) Let’s consider the following log linear model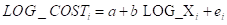
Explain the coefficient of b and find the elasticity of number of server on the total cost.
6) Linear and Nonlinear Polynomial Models (1 point each)
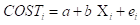
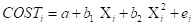
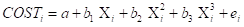
a. Estimate the model and copy and paste the results and perform the F test for each model
b. Let’s compare the two models, the Linear vs. Nonlinear models. In terms of goodness-to-fit, which one fits better? Carefully explain.
c. According to each model, what are the total cost to maintain the facility if you want install 10, 20, 50 servers?
d. Choose the best model from the regression model in terms of goodness-to-fit, and find the number of servers to minimize the total cost of the service facility.
II. Single Family House Sales in Chicago
We obtain a house sales data from the local Multiple Listing Service (MLS) who provides the up-to-date real estate market listing prices. We obtain the following variables from the properties listed in Chicago in 2015.
BEDROOM : Number of Bedroom
BATHROOM : Number of Bathroom
SQFT : Square Feet of Living Area
GARAGE : Number of Cars in Garage
AGEBLD : Age of Building
FIREPLACE : Number of Fireplace
ZIP : Zip Code
PRICE : Listing Price
- Find the descriptive statistics of Listing Price (PRICE) for two zip codes separately, and compare their central tendency, and variance using the following hypothesis tests: (1 points each)
- Simple Regression Model (Estimate separate model for each zip code)
Let’s consider the following simple regression model:
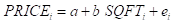
1) Estimate the simple regression model, and copy and paste the results from Minitab Regression output from Minitab and explain the meaning of coefficients from each model. (1 point)
2) Using the simple regression output find the following statistics. (0.5 point each)
) Estimate the simple regression model, and copy and paste the results from Minitab Regression output from Minitab and explain the meaning of coefficients from each model. (1 point)
2) Using the simple regression output find the following statistics. (0.5 point each)
Statistics ZIP CODE 1 = ZIP CODE2 =
a. Estimated intercept
b. Estimated slope coefficient
c. Total Sum of Square (TSS)
d. Regression Sum of Square (RSS)
e. Error Sum of Square (ESS)
f. R2
g. Adjusted R2
h. Variance and standard error of b1
i. Correlation Coefficient between listing price (PRICE) and square feet (SQFT)
j. Variance of et
- Nonlinear Model (Estimate separate model for each zip code, 1 point each)
Let’s consider the following log transformed model.
1) Estimate the model and copy and paste the results, and explain the meanings of the estimated slope coefficients from each regression model.
2) Compare and explain the elasticity of square feet to price between two zip codes, which is
- Multiple Regression Model (Estimate separate model for each zip code, 1 points each)
1) Estimate the model using Minitab, and copy and paste the results.
2) Explain the meanings of the estimated coefficients.
3) Perform the t tests to find which variables are significant. List all significant variables at 5% and 10% significance levels.
4) Perform the F test for the each regression model, explain your verdict from the test.
5) Let’s compare the simple regression and the multiple regression models for each zip code. Carefully explain which is better.
6) Challenging model (3 points)
Now let’s find the best model to explain the listing price using the given variables. Any combination or any different functional forms are allowed. Find the best possible model. After deciding your final model, justify why your model is better than the other models.