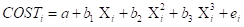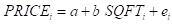Open University Statistics M248 TMA 04
Faculty of Science, Technology, Engineering and MathematicsM248 Analysing data
M248 - TMA 04
*Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.
You are advised to look at the general advice on answering TMAs provided on the M248 website. Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions. Note that one of the Minitab files that you require for TMA 04 is not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website. For your convenience, the other Minitab file required for TMA 04, which already appeared in the module, is also available for download from the ‘Assessment’ area.*
Question 1, which covers topics in Unit 7, and Question 2, which covers topics in Unit 8, form M248 TMA 04. Question 1 is marked out of 23; Question 2 is marked out of 27.
Question 1 { 23 marks
You should be able to answer this question after working through Unit 7.
(a) Let X and Y be independent random variables both with the same
mean µ 6= 0. Define a new random variable W = aX + bY where a and
b are constants.
(i) Obtain an expression for E(W). [2]
(ii) What constraint is there on the values of a and b so that W is an
unbiased estimator of µ? Hence write all unbiased versions of W as
a formula involving a, X and Y only (and not b). [3]
(b) An otherwise fair six-sided die has been tampered with in an attempt to
cheat at a dice game. The effect is that the 1 and 6 faces have different
probability of occurring than the 2, 3, 4 and 5 faces.
Let θ be the probability of obtaining a 1 on this biased die. Then, the
outcomes of rolling the biased die have the following probability mass
function.
Table 1 The p.m.f. of outcomes of rolls of a biased die: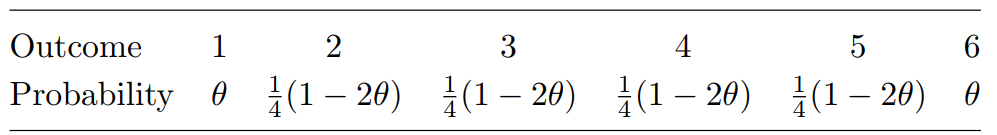
(i) By consideration of the p.m.f. in Table 1, explain why it is necessary for θ to be such that 0 < θ < 1=2. [2]
(ii) The value of θ is unknown. Data from which to estimate the value of θ were obtained by rolling the biased die 1000 times. The result of this experiment is shown in Table 2.
Table 2 Outcomes of 1000 independent rolls of a biased die
Show that the likelihood of θ based on these data is
L(θ) = C θ395 (1 − 2θ)605 where C is a positive constant, not dependent on θ. [5]
(iii) Show that L0(θ) = C θ394(1 − 2θ)604 (395 − 2000 θ): [4]
(iv) What is the value of the maximum likelihood estimate, θb, of θ based on these data? Justify your answer. What does the value of θb suggest about the value of θ for this biased die compared with the
value of θ associated with a fair, unbiased, die? [4]
c) Studies of the size and range of wild animal populations often involve tagging observed individual animals and recording how many times each is caught in a trap (from which it is then released back into the wild). The dataset presented in Table 3 consists of the numbers of times each of n = 334 wood mice were caught in a particular trap (over a two-year time period). The data are also provided in the Minitab file wood-mice.mtw.
Table 3 Numbers of trappings of wood mice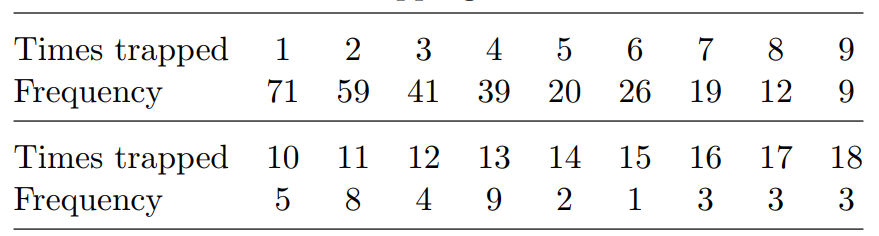
The geometric distribution with parameter p is a good model for these data.
(i) What is the maximum likelihood estimator of p for a geometric model? [1]
(ii) What is the maximum likelihood estimate of p for the data in Table 3? You are recommended to use Minitab to help you to answer this part of the question. [2]
Question 2 in Statistics
You should be able to answer this question after working through Unit 8.
(a) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)
Modern aircraft cockpit windscreens are complex items, comprising several layers of material and a heating system. Such windscreens are replaced upon damage to any of their components. A dataset was collected on the times to replacement of n = 84 windscreens of a particular modern airliner. The sample mean windscreen replacement time was 23 515 hours of flight. The sample standard deviation of windscreen replacement times was 5168 hours of flight.
(i) Obtain an approximate 90% confidence interval for the mean replacement time of this type of aircraft windscreen. What
property of the dataset justifies using this type of confidence interval, and why? [6]
(ii) Interpret the particular confidence interval that you found in part (a)(i) in terms of repeated experiments. [3]
(b) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)
In a large study of patients who were being treated for hypertension (high blood pressure), 148 out of 5493 patients receiving the conventional treatment for hypertension later suffered a stroke. Also,
192 out of 5492 patients receiving an alternative drug to treat their hypertension later suffered a stroke
(i) Obtain an approximate 95% confidence interval for the difference in proportions between the number of conventionally treated hypertension patients who later suffered a stroke and the number of hypertension patients treated with the alternative drug who later suffered a stroke. (You are advised to work with proportions rounded to four decimal places throughout; also, you may assume that the numbers involved are large enough that your approximation is a good one.) [5]
(ii) Some clinicians had suggested that the proportions of hypertension patients who suffered a stroke would not depend on which treatment they were being given. Are the data consistent with that
suggestion? Justify your answer briefly. [2]
(c) In various places in this module, data on the silver content of coins minted in the reign of the twelfth-century Byzantine king Manuel I Comnenus have been considered. The full dataset is in the Minitab file coins.mtw. The dataset includes, amongst others, the values of the silver content of nine coins from the first coinage (variable Coin1) and seven from the fourth coinage (variable Coin4) which was produced a number of years later. (For the purposes of this question, you can ignore the variables Coin2 and Coin3.) In particular, in Activity 8 and Exercise 2 of Computer Book B, it was argued that the silver contents in both the first and the fourth coinages can be assumed to be normally distributed. The question of interest is whether there were differences in the silver content of coins minted early and late in Manuel’s reign. You are about to investigate this question using a two-sample t-interval.
(i) Using Minitab, find either the sample standard deviations of the two variables Coin1 and Coin4, or their sample variances. Hence, check for equality of variances using the rule of thumb given in
Subsection 4.4 of Unit 8. [3]
(ii) Whatever the outcome of part (c)(i), use Minitab to obtain a 90% two-sample t-interval for the difference E(X1) − E(X4) where X1 denotes the mean silver content in coins of the first coinage and X4
denotes the mean silver content in coins of the fourth coinage.
State that interval and comment briefly on what it tells us about the silver content of coins in the earlier and later coinages. [3]
(iii) Name the distribution used in constructing the confidence interval in part (c)(ii), state the value of its parameter and show why the parameter takes the value that it does. [2]
(iv) What would have been the outcome if you had obtained a 90% two-sample t-interval for E(X4) − E(X1) instead of for
E(X1) − E(X4)? Justify your conclusion in terms of the derivative of the parameter transformation involved. [3]
If you need someone to help you with this statistics assignment, then MyMathLab homework help is the right platform to address all your statistics needs.