Write R code to plot this pdf for various values of b
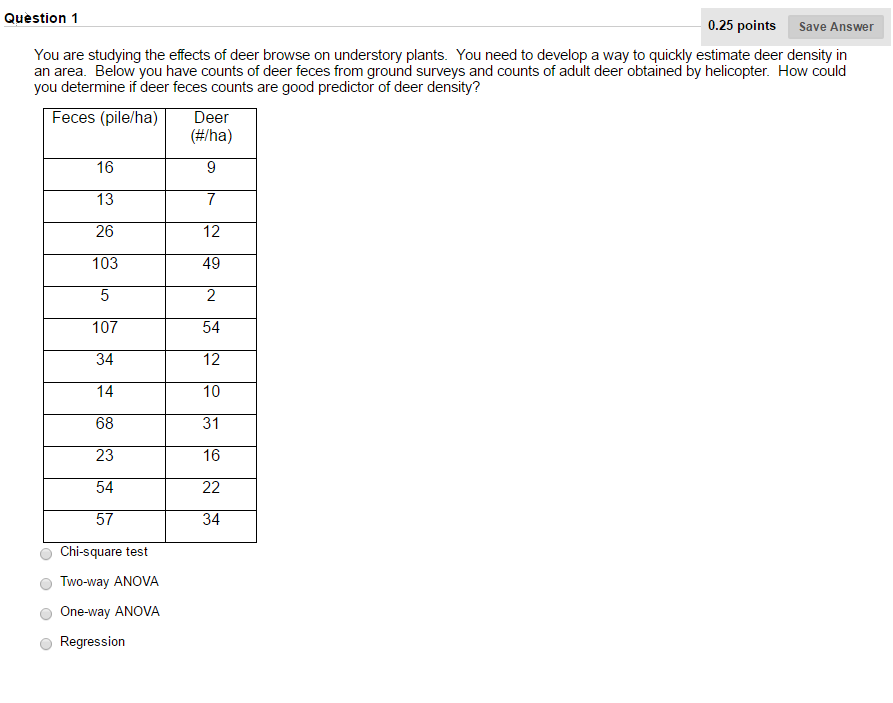
Sample assignment on R statistics help
Answer all questions. Marks are indicated beside each question. You should submit your solutions before the
You should submit both
• a .pdf file containing written answers (word processed, or hand-written and scanned), and
• an .R file containing R code.
For all answers include
• the code you have written to determine the answer, the relevant output from this code, and a justification of how you got your answer.
• Total marks: 60 1. Consider the one parameter family of probability density functions
fb for − b ≤ x ≤ bwhere b > 0.
(a) Write R code to plot this pdf for various values of b > 0. [2 marks]
(b) Determine the method of moments estimator for the parameter b. (No R code necessary) [4 marks]
(c) Determine the Likelihood function for the parameter b. By writing R code to plot a suitable graph, determine that the derivative of this likelihood function is never zero. [4 marks] (d) Hence find the Maximum Likelihood Estimator for the parameter b. (No R code necessary) [4 marks] (e) The data in the file Question 1 data.csv contains 100 independent draws from the probability distribution with pdf fb(x), where the parameter b is unknown. Load the data into R using the command
D <- read . csv (path_to_f i l e )$x
where path_to_file indicates the path where you have saved the .csv file
e.g. path_to_file = “c:/My R Downloads/Question 1 data.csv”
Note that forward slashes are used to indicate folders (this is not consistent with the usual syntax for Microsoft operating systems).
Write R code to calculate an appropriate Method of Moments Estimate and a Maximum Likelihood Estimate for the parameter b, given this data. [4 marks]
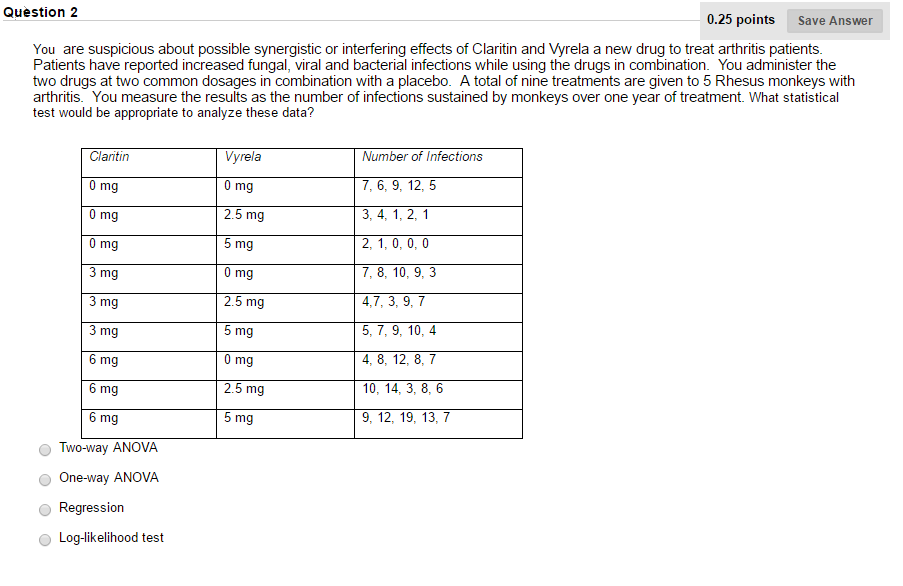
- The data in the file Question 2 data.csv is thought to be a realisation of Geometric Brownian Motion
St = S0eσWt+µt
where Wt is a Wiener process and σ,µ and S0 are unknown parameters. Load the data into R using the command
S <- read . csv (path_to_f i l e )
where path_to_file indicates the path where you have saved the .csv file.
(a) Write R code to determine the parameter S0. [2 marks]
(b) Write R code to determine if Geometric Brownian Motion is suitable to model this data.
You may do this by
• plotting an appropriate scatter plot/histogram, and/or • using an appropriate statistical test.
[6 marks]
(c) Write R code to determine an estimate for µ and σ2 using Maximum Likelihood Estimators.
(You do not have to derive these estimators). [5 marks] - The data in the file Question 3 data.csv is a matrix of transition probabilities of a Markov Chain. Load the data into R using the command
P <- as . matrix ( read . csv (path_to_f i l e ))
with an appropriate value for path_to_file.
(a) Verify that this Markov Chain is ergodic. (No R code necessary) [4 marks]
(b) Suppose that an initial state vector is given by
x=(0.1,0.2,0.4,0.1,0.2) (1)
Write R code to determine the state vector after 10 time steps. Do this without diagonalising the matrix
P. [3 marks]
(c) Write R code to verify this answer by diagonalising the matrix P. Note that the eigen(A) function produces the right-eigenvectors of a matrix A (solutions of Av = λv) However we want the left-eigenvectors (solutions of vA= λv).
These are related by
v is a left-eigenvector of A if and only if vT is a right-eigenvector of AT.
[8 marks]
(d) Hence, or otherwise, determine the limiting distribution with the initial state vector given in (1).
[4 marks] - The data if the file Question 4 data.csv is a generator matrix for a Markov Process. Load the data into R using the command
A <- as . matrix ( read . csv (path_to_f i l e ))
with an appropriate value for path_to_file.
(a) Suppose that X0 =0. Write R code to simulate one realisation of the Markov Process Xt. The output should be two vectors (or one data frame with two variables).
• The first vector indicates transition times.
• The second vector indicates which state the Markov Process takes at this time (i.e. one of 0,1,2,3,4).
How to proceed:
• The first line of your code must read
set . seed (4311)
to ensure that this realisation is repeatable.
• For each Xt you must determine
– what the transition time s to the next state is,
– what the probabilities to transfer to each state are, and hence randomly select a suitable value for Xt+s.
[9 marks] (b) Write R code to plot an appropriate graph that describes this realisation. [1 mark]