The Open University Statistics TMA02

Question 1 - 27 marks
You should be able to answer this question after working through Unit 3.
(a) In 1986, the US Space Shuttle Challenger tragically exploded in flight. This accident was caused by the catastrophic failure of rubber ‘O-ring’ seals that linked segments of its rocket boosters together. There were six O-ring seals in Challenger (and all other Space Shuttles at the time). Table 1 shows the numbers of O-ring seal failures that had occurred on each of 23 previous Space Shuttle flights.

Table 1 Number of O-ring seal failures

(i) Let p be the probability that an O-ring seal fails on a flight. What distribution is appropriate to describe the failure or non-failure of a particular O-ring seal on a particular flight? (Ensure that you
define the corresponding random variable appropriately.)

(ii) A reasonable estimate of p is 3=46 ’ 0:065. Explain where this number comes from.

(iii) It is suggested that an appropriate model for the number of O-ringseals that fail on a particular flight might be a binomial distribution B(6; p). What assumptions are made by using thismodel? In your opinion, is a binomial model appropriate? Briefly justify your answer.

iv) Use Minitab to obtain a table containing both the p.m.f. and c.d.f. of the B(6; p) distribution with p = 0:065. (Do not change the number of decimal places of the values obtained from those provided by Minitab.)

(v) Use the information in Table 1 and the solution to part (a)(iv) to complete the following table, giving your values rounded to three decimal places.

Comment briefly on how close the observed proportions of flights on which 0; 1; 2; : : : ; 6 O-ring seals failed are to those predicted by the binomial model. What does this suggest about the appropriateness, or otherwise, of the binomial model?

(b) Records show that 6% of blood samples tested for a certain condition test positive. Assuming that whether or not a blood sample tests positive is independent of whether or not any other blood sample tests
positive, calculate by hand the following probabilities correct to four decimal places. In each case, state clearly the probability model that you use (including the values of any parameters) and show your working.

(i) The probability that, out of 20 samples tested, at least three will test positive. [6]
(ii) The probability that the first blood sample that tests positive tomorrow will be the ninth sample tested. [3]

(c) The number of flaws in a fibre optic cable follows a Poisson distribution with parameter λ = 1:25. Calculate by hand the probability that there are two or fewer flaws in such a fibre optic cable, giving your answer correct to three decimal places. Show your working.

Question Two
You should be able to answer this question after working through Unit 4.
(a) In Question 2(b) of TMA 01, the probability mass function of a discrete random variable X representing the number of bicycles available at a docking station each morning was introduced. This p.m.f. is repeated
here, in Table 2.

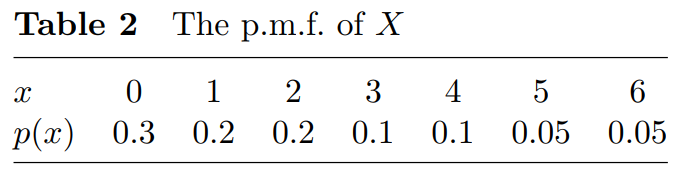
(i) What is the mean number of bicycles available at the docking station each morning? [2]
(ii) What is the variance of the number of bicycles available at the docking station each morning?

(b) The Atacama Desert in Chile is known as the driest place on Earth. Suppose that in one part of the Atacama Desert, whether it rains at all in a given year has probability 0.2 and that whether or not it rains in one year is independent of whether or not it rains in any other year.

Answer the following questions, in each case stating clearly the probability model that you use (including the values of any parameters).

(i) Suppose that a random variable X is defined to take the value 1 when there is rainfall in a particular year and 0 when there is not.
What is the mean of the random variable X? [2]
(ii) What is the expected number of years with some rainfall in a period of 100 years? [2]
(iii) What is the expected value of the number of years up to and including the first year in which there is some rainfall? [2

(c) A scout on a camping trip is requested to find some dry sticks of length
at most one metre to use as firewood. A model for the distribution of
the lengths, X, in metres, of sticks that she brings back to the camp has
probability density function
f(x) = 3
2
px; 0 < x < 1:
(i) According to the model, what is the mean length of the sticks that the scout brings back? [3]
(ii) According to the model, what is the standard deviation of the lengths of the sticks that the scout brings back? [5]
(iii) What are the units of the mean and the standard deviation that you have just calculated? [1]

(d) The number of customers buying a cooked breakfast at a high-street cafe on a weekday morning is a random variable X with mean 24 and variance 36. As a loss leader { a product sold at a loss to attract
customers to also partake of its other offerings { the cafe charges $3:50 per breakfast and has fixed breakfast-specific daily costs (ingredients, labour) of $105. Let Y be the cafe’s daily loss on breakfasts, in pounds, where Y = 105 − 3:5X: What are the mean and standard deviation of this loss? [3]

Solution for the first question has been attached here for your reference, TMO2 Open university statistics.docx
Let us no if you need further help with your statistics.

Solve using Excel & Minitab (Do not use formula)

The following questions are from probability and statistics questions. The questions were previously solved by our statistic experts using MINITAB; in case you are a student looking for help with similar questions, then you can contact us so that we may provide similar services under our do MyMathLab homework so that we can provide you similar solutions, or solutions with similar questions, either using Excel data analysis tools , or by using the latest Minitab application software. The solutions to each question are attached for you confirmation.

1. A die is tossed 3 times. What is the probability of
   (a) No fives turning up?
   (b) 1 five?
   (c) 3 fives?
   Probability Solution for Question 1
   Outut for Question 1:
   Probability Density Function

Binomial with n = 3 and p = 0.17

x P( X = x )
0 0.571787
Probability Density Function
Binomial with n = 3 and p = 0.17
x P( X = x )
1 0.351339
Probability Density Function
Binomial with n = 3 and p = 0.17
x P( X = x )
3 0.004913

2. Hospital records show that of patients suffering from a certain disease, 75% die of it. What is the probability that of 6 randomly selected patients, 4 will recover?

   Question 2
   probability of 4 recoveries
   Probability Density Function
   Binomial with n = 6 and p = 0.25
   x P( X = x )
   4 0.0329590

3. The ratio of boys to girls at birth in Singapore is quite high at 1.09:1.
   What proportion of Singapore families with exactly 6 children will have at least 3 boys? (Ignore the probability of multiple births.)

Question 3
Probability of atleast 3 Boys
Cumulative Distribution Function
Binomial with n = 6 and p = 0.5219
x P( X ≤ x )
2 0.303638
P(x <= 3) = 1-0.3036 = 0.6957

4. A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain
   (a) no more than 2 rejects? (b) at least 2 rejects?

   Question 4

   a) Probability of not more than 2
   Cumulative Distribution Function
   Binomial with n = 10 and p = 0.12
   x P( X ≤ x )
   2 0.891318

b) probability of at least 2 = 1-P(x <= 1)
Cumulative Distribution Function
Binomial with n = 10 and p = 0.12
x P( X ≤ x )
1 0.658275
p(x>=2) = 1-0.6583 = 0.3417

5. A die is rolled 240 times. Find the mean, variance and standard deviation for the number of 3s that will be rolled?

6. If there are 200 typographical errors randomly distributed in a 500 page manuscript, find the probability that a given page contains exactly 3 errors.

   Question 6

   exactly 3 errors.
   Results for: Q6.MTW
   Probability Density Function
   Poisson with mean = 0.4
   x P( X = x )
   3 0.0071501

7. A sales form receives on the average of 3 calls per hour on its toll-free number. For any given hour, find the probability that it will receive a. At most 3 calls; b. At least 3 calls; and c. Five or more calls.

Question 7

At most 3 calls
P (X <= 3)
Cumulative Distribution Function
Poisson with mean = 3
x P( X ≤ x )
3 0.647232
b At Least 3 Calls = 1-P(X<=2)
Cumulative Distribution Function
Poisson with mean = 3
x P( X ≤ x )
2 0.423190
p(X>=3) = 1-0.42319 = 0.5768
c Probability of five or More calls
= 1- p(X<=4)
Cumulative Distribution Function
Poisson with mean = 3
x P( X ≤ x )
4 0.815263
p(x>=5) = 1-0.815263 = 0.1847

8. A life insurance salesman sells on the average 3 life insurance policies per week. Calculate the probability that in a given week he will sell
   a. Some policies
   b. 2 or more policies but less than 5 policies.
   c. Assuming that there are 5 working days per week, what is the probability that in a given day he will sell one policy?

A solution to this probability question has been provided by our experts, you may contact us if you need help with this question.

9. Twenty sheets of aluminum alloy were examined for surface flaws. The frequency of the number of sheets with a given number of flaws per sheet was as follows:

Number of flaws
Frequency
0 4
1 3
2 5
3 2
4 4
5 1
6 1
What is the probability of finding a sheet chosen at random which contains 3 or more surface flaws?

10. Find the area right of z=1.11

You can solve this question using either Excel data analysis tools, or Minitab, when you choose to use Excel, then use the function =NORM.S.DIST(1.11,TRUE) = 0.8665, which gives you the area to the left, to find the area to the right = 1-0.8665 = 0.1335

11. Find the area left of z = -1.93
    You can also apply similar tactics as above to solve this question.
12. Find the area between -/+ 1, 2, 3, 4, 5, 6, standard deviations.

13. Find the z value such that the area under the normal distribution curve between 0 and the z value is 0.2123
14. A study on recycling shows that in a certain city, each household accumulates an average of 14 pounds of newspaper each month to be recycled. The standard deviation is 2 pounds. If a household is selected at random, find the probability it will accumulate the following:
    a. Between 13 and 17 pounds of newspaper for a month.
    b. More than 16.2 pounds of newspaper for one month.

This question has been solved in many of our questions under our myMathlab homework help services.

15. A standardized achievement test has a mean of 50 and a standard deviation of 10. The scores are normally distributed. If the test is administered to 800 selected people, approximately how many will score between 48 and 62?