Show that the likelihood of θ for these data has the form

This question is intended to assess your understanding of point estimation.
You should be able to answer this question after working through Unit D1.
(a) The data in Table 4 relate to the classification of 134 recorded crimes(occurring during a month in a certain UK postcode area) into five crime categories.

Table 4    Classification of crimes
 Crime categories    1    2    3    4    5
Observed frequency    25    14    42    11    42

A possible model for these data is the one indexed by a parameter θ, where 0 < θ < 1, with the following probabilities of categories 1,2,3,4,5, respectively: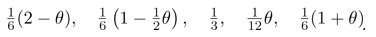

(i) Show that the likelihood of θ for these data has the form
,
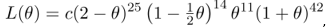where c is a number and does not involve θ. (You should show how
c is formed, but you do not need to evaluate its value.)
(ii) Ignoring c, the log-likelihood is [4]
.
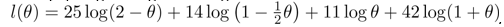Use MINITAB to evaluate l(θ) at θ = 0.05,0.10,0.15,... ,0.95.
Give the values of l(θ) in a table, and produce a graph in which
l(θ) is plotted against θ for each of these values.
(iii) Correct to two decimal places, the value of θ that maximizes l(θ) is 0.90. Find θb, the maximum likelihood estimate of θ, correct to three decimal places. Include sufficient detail in your answer to [6]