Lesson Chapter 5 Review Questions
Qn1. Charity is planting trees along her driveway, and she has 6 pine trees and 6 willows to plant in one row. What is the probability that she randomly plants the trees so that all 6 pine trees are next to each other and all 6 willows are next to each other? Express your answer as a fraction or a decimal number rounded to four decimal places.
Q2. A person rolls a standard six-sided die 12 times. In how many ways can he get 6 fours, 5 ones, and 1 two?
Qn3. A card is drawn from a standard deck of 52 playing cards. What is the probability that the card will be a heart and not a seven? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn4. You are going to play mini golf. A ball machine that contains 21 green golf balls, 18 red golf balls, 23 blue golf balls, and 17 yellow golf balls, randomly gives you your ball. What is the probability that you end up with a blue golf ball? Express your answer as a simplified fraction or a decimal rounded to four decimal places.
Qn6.
A newspaper company classifies its customers by gender and location of residence. The research department has gathered data from a random sample of 1738
customers. The data is summarized in the table below.
Probability Distribution Table
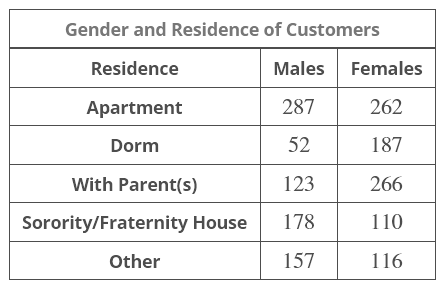
What is the probability that a customer is female? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn7. A coin is tossed 3 times. What is the probability that the number of tails obtained will be 1? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn8. f a coin is tossed 5 times, and then a standard six-sided die is rolled 4 times, and finally a group of two cards are drawn from a standard deck of 52 cards without replacement, how many different outcomes are possible?
If a coin is tossed 5 times, and then a standard six-sided die is rolled 4 times, and finally a group of two cards are drawn from a standard deck of 52
cards without replacement, how many different outcomes are possible?
You can also solve this using technology.
Use The Fundamental Principle of Counting with the Combination Rule.
The experiments or tasks in this problem can be grouped into three basic types of activities, namely, tossing a coin 5
times, rolling a standard six-sided die 4
times, and drawing two cards from a deck of cards without replacement. To obtain the solution to the problem, the number of possible outcomes for each task is computed and then the Fundamental Principle of Counting is applied to the three tasks.
There are 25
outcomes possible when tossing a coin 5 times, 64 outcomes possible when rolling a standard six-sided die 4 times, and C252
outcomes possible when drawing two cards from a deck of cards without replacement. Applying the Fundamental Principle of Counting to these three tasks, we see that the total number of different outcomes possible is
25⋅64⋅C252=32⋅1296⋅1326=54991872
.Qn9.
6 cards are drawn from a standard deck without replacement. What is the probability that at least one of the cards drawn is a black card? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn11. In a history class there are 8 history majors and 8 non-history majors. 4 students are randomly selected to present a topic. What is the probability that at least 2 of the 4 students selected are non-history majors? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn12.
Jill is ordering pizza at a restaurant, and the server tells her that she can have up to three toppings: black olives, chicken, and spinach. Since she cannot decide how many of the toppings she wants, she tells the server to surprise her. If the server randomly chooses which toppings to add, what is the probability that Jill gets just spinach? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn13.
There are 77 students in a history class. The instructor must choose two students at random.
Academic Year History majors non-History majors
Freshmen 13 5
Sophomores 2 9
Juniors 12 12
Seniors 14 10
What is the probability that a junior non-History major and then another junior non-History major are chosen at random? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn14.
Customer account "numbers" for a certain company consist of 3 letters followed by 5 numbers.
Step 1 of 2 : How many different account numbers are possible if repetitions of letters and digits are allowed?
Qn15.
A coin is tossed 6 times. What is the probability that the number of heads obtained will be between 4 and 6 inclusive? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn16. A mail order company classifies its customers by gender and location of residence. The research department has gathered data from a random sample of 1936 customers. The data is summarized in the table below.
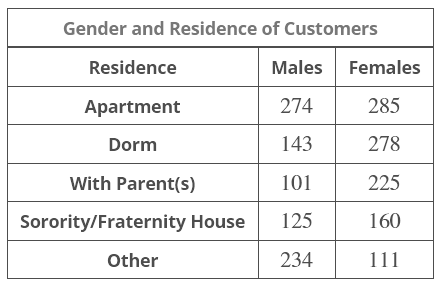
What is the probability that a customer lives in a dorm? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn18. A bag contains 9 red, 8 orange, and 7 green jellybeans. What is the probability of reaching into the bag and randomly withdrawing 16 jellybeans such that the number of red ones is 5, the number of orange ones is 7, and the number of green ones is 4? Express your answer as a fraction or a decimal number rounded to four decimal places.
Qn19.
Larissa is ordering apple pie at a restaurant, and the server tells her that she can have up to four toppings: walnuts, pecans, whipped cream, and caramel. Since she cannot decide how many of the toppings she wants, she tells the server to surprise her. If the server randomly chooses which toppings to add, what is the probability that Larissa gets just walnuts and pecans? Express your answer as a fraction or a decimal number rounded to four decimal places.



